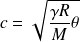Célérité Acoustique (en savoir plus)
Célérité acoustique et température
L'air peut être considéré comme un gaz parfait diatomique
Pour un gaz parfait,
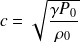
Or, la loi des gaz parfaits fournit :
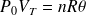
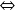
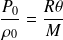
avec
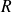: constante des gaz parfaits (
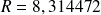J.mol-1.K-1)
et
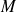: masse molaire de l'air, (
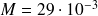kg.mol-1)
On peut alors en déduire la dépendance de la célérité avec la température :
En traçant et en calculant les valeurs de la célérité avec des températures raisonnables pour des applications acoustiques sous nos latitudes, la relation entre température et célérité est donnée dans le tableau et montrée à la figure ci-dessous :
Température ( C)
Célérité (m.s-1)
-5
328.5
0
331.5
5
334.5
10
337.5
15
340.5
20
343.4
25
346.3
30
349.2
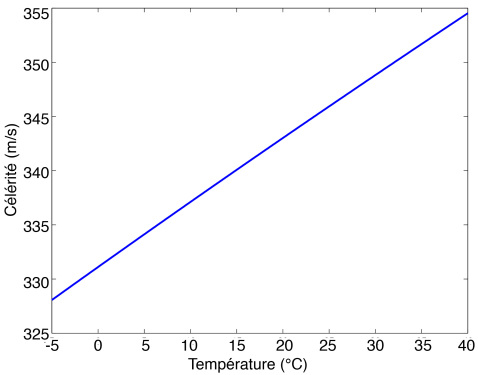
L'oeil avisé remarquera que la courbe ne ressemble pas franchement à une loi en racine, c'est tout simplement dû au fait que la température est en Kelvin, ce qui décale le zéro de 273,15 degrés, et la portion tracée à nos températures usuelles ne correspond donc qu'à une toute petite zone de la courbe, qui apparaît comme "linéarisée" par ce décalage de température.
