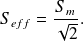RMS and average values
For time dependant signals, it can be useful to know their characteristics over a certain observation time
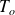. The following values are the most commonly used characteristics.
The maximum and minimum values of the signal
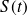are respectively the highest and lowest points of the signal over a period
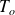.The average
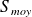of a signal is given by :
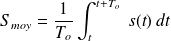.The RMS value of a signal is given by :
.
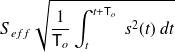Remarque : Remark
For periodic signals, the RMS and average value are calculated over a whole number of periods.
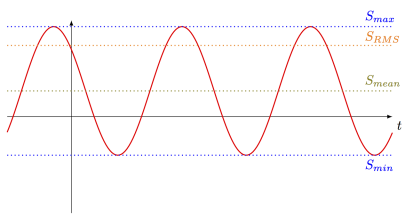
Illustration for a sine wave with a continuous component (DC) equal to
:
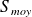Exemple : Example
Calculate the RMS value of the signal
.
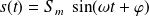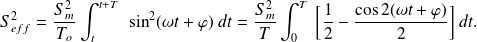
The integral of
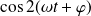is equal to zero, as it is done over two periods.
We therefore have :
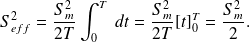
Finally, we obtain :
