Modèle de couplage piézoélectrique simplifié
L'effet piézoélectrique peut s'avérer relativement complexe, faisant intervenir des tenseurs de couplage déformation / champ électrique d'ordres élevés.
pour rendre le couplage piézoélectrique plus aisé à modéliser, il est fait ici plusieurs approximations
petites déformations, permettant de linéariser les équations de couplage
le matériau piézoélectrique présente une épaisseur négligeable devant ses dimensions transversales. Ainsi on peut assimiler une face du matériau (lame) piézoélectrique comme une armature mobile d'un condensateur, dont l'autre extrémité est supposée immobile (à l'instar du transducteur électrostatique)
l'élément piézoélectrique ne subit que des forces de traction, à l'exclusion de toute autre contrainte dans le plan transverse.
On considérera dans ce qui suit :
un élément de matériau piézoélectrique mince et section carrée, soumis à des forces de traction-compression harmoniques (de fréquence
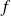 ) dans son épaisseur (et pas des forces normales à sa surface, comme présenté dans les cours G3.2 et G3.3), entraînant un mouvement vibratoire transversal ;
) dans son épaisseur (et pas des forces normales à sa surface, comme présenté dans les cours G3.2 et G3.3), entraînant un mouvement vibratoire transversal ;
les deux faces peuvent être considérées comme les 2 armatures d'un condensateur, dont la charge varie dans le temps en fonction du déplacement de l'armature mobile
nous considèrerons le cas des petites déformations, et si ses dimensions latérales sont petites devant la longueur d'onde dans le matériau (
 ), on peut supposer en première approximation que la lame piézoélectrique se comporte principalement comme une compliance (ou souplesse) mécanique
), on peut supposer en première approximation que la lame piézoélectrique se comporte principalement comme une compliance (ou souplesse) mécanique
 .
.
GRANDEURS PHYSIQUES CONSIDÉRÉES
Dans ce qui suit, nous noterons :
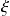 l'élongation de la face supérieure ;
l'élongation de la face supérieure ; la vitesse vibratoire de la face supérieure ;
la vitesse vibratoire de la face supérieure ;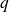 la charge électrique de l'élément ;
la charge électrique de l'élément ; la courant électrique traversant l'élément ;
la courant électrique traversant l'élément ; la tension appliquée entre les armatures ;
la tension appliquée entre les armatures ;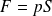 la force de traction appliquée à l'élément.
la force de traction appliquée à l'élément.
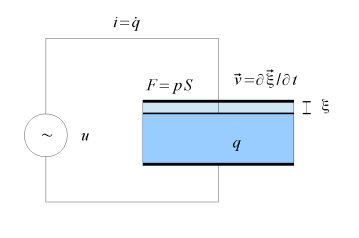
La charge électrique
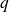 , due à la polarisation électrique provoquée par la déformation résultant de l'application de la force
, due à la polarisation électrique provoquée par la déformation résultant de l'application de la force
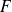 seule (ie. lorsque le piezo est en circuit ouvert), peut s'exprimer, dans l'hypothèse linéaire :
seule (ie. lorsque le piezo est en circuit ouvert), peut s'exprimer, dans l'hypothèse linéaire :
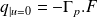
où
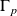 désigne le module piézoélectrique de charge en C/N.
désigne le module piézoélectrique de charge en C/N.
Réciproquement, l'application à l'élément de la tension
 seule (ie. lorsque le bilame n'est pas soumis à une force extérieure) y crée un champ électrique, résultant en une contrainte, et par voie de conséquence une déformation de la face mobile selon :
seule (ie. lorsque le bilame n'est pas soumis à une force extérieure) y crée un champ électrique, résultant en une contrainte, et par voie de conséquence une déformation de la face mobile selon :
où
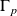 est cette fois exprimée en m/V.
est cette fois exprimée en m/V.
Remarque :
il est important de noter que, contrairement à la transduction électrostatique qui est caractérisée par des équations quadratiques (non linéaires), les relations de couplage piézoélectrique sont linéaires.
ÉQUATIONS DU MOUVEMENT
Loi de Newton : en première approximation, le bilame se comporte comme une souplesse mécanique dans le domaine fréquentiel de fonctionnement du transducteur (ie. en dessous de la fréquence de résonance de la plaque). Lorsque le bilame n'est soumis qu'à la force
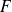 (en supposant le piezo en circuit ouvert), le bilame opposera une force de rappel de telle manière que :
(en supposant le piezo en circuit ouvert), le bilame opposera une force de rappel de telle manière que :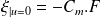
Loi des mailles : Si le transducteur piézo, assimilé en première approximation à un condensateur de capacité
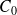 , est connecté à une source de tension
, est connecté à une source de tension
 , on a la loi suivante :
, on a la loi suivante :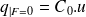
ÉQUATIONS DE COUPLAGE PIÉZOÉLECTRIQUE SIMPLIFIÉ
Si l'élément est soumis simultanément à une tension
 et à une force
et à une force
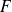 , la déformation résultante est la combinaison de la déformation à force
, la déformation résultante est la combinaison de la déformation à force
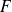 nulle et de la déformation à tension
nulle et de la déformation à tension
 nulle (en supposant que la lame se comporte comme compliance mécanique
nulle (en supposant que la lame se comporte comme compliance mécanique
 pure), selon
pure), selon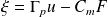
Réciproquement, la charge électrique
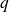 de la lame résulte de la combinaison
de la lame résulte de la combinaisonde la conversion piézoélectrique à tension
 nulle, et de l'application de la
nulle, et de l'application de latension seule
 à travers la capacité électrique
à travers la capacité électrique
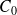 statique selon
statique selon
À l'instar des grains 3.2 et 3.3, nous cherchons à relier les grandeurs
mécaniques
 aux grandeurs électriques
aux grandeurs électriques
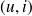 . Cela revient donc à dériver
. Cela revient donc à dériverles deux précédentes équation, afin d'obtenir

Problème : dans le précédent système, le couplage est exprimé à travers un coefficient imaginaire pur
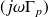 , qui ne peut être représenté dans un schéma par un élément de type transformateur (de coefficient réel). Nous allons donc réarranger le système précédent de deux manières différentes
, qui ne peut être représenté dans un schéma par un élément de type transformateur (de coefficient réel). Nous allons donc réarranger le système précédent de deux manières différentesFormulation 1 :
Si on dérive
 d'après le système précédent, on montre que :
d'après le système précédent, on montre que :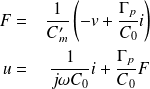
où
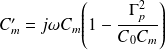
Le couplage est désormais exprimé par le coefficient
 .
.Formulation 2 :
Si on dérive
 d'après le système précédent, on montre que :
d'après le système précédent, on montre que :
où
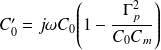
Le couplage est désormais exprimé par le coefficient
 .
.






