Equations de comportement
Partant des équations de comportement d'un portion de tube
et considérant les hypothèses de constantes localisées, il vient
où la pression
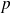et la vitesse
sont observées au milieu de l'élément.
Les équations approchées de comportement du tube s'écrivent ainsi sous la forme :
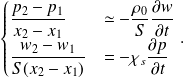
Pour une onde plane harmonique à pulsation
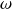, les dérivées temporelles s'écrivent
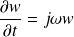et
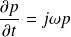. Les équations s'écrivent ainsi
où
est le volume du tube
.
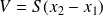