Constantes localisées
Définition :
Les hypothèses utilisées s'appellent les hypothèses de constantes localisées. Ces hypothèses sont vérifiées lorsque la longueur d'onde est très grande devant la plus grande des dimensions d'un objet. Dans le cas d'un tube de longueur
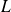, elles se traduisent mathématiquement par
, où
est le nombre d'onde, soit
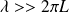, où
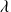est la longueur d'onde.
Exemple :
Exemple 1 : pour un tube de longueur 10 cm, on considère que les basses fréquences sont dans la gamme 0 - 3000 Hz.
Exemple 2 : pour un tube de longueur 1 m, on considère que les basses fréquences sont dans la gamme 0 - 300 Hz.
Complément :
Conséquences
Le problème étudié est ici un problème à une dimension, l'onde est plane.
Les grandeurs physiques connaissent des variations linéaires entre l'entrée et la sortie du tube. Les dérivées partielles peuvent s'écrire comme des différences finies.
Ceci permet de ne considérer que les grandeurs physiques en entrée et en sortie de tube (et pas en tout point du tube comme on doit le faire pour un tube long devant la longueur d'onde).
